① 格兰杰。姓
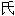。②
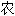
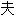。Clive W.J. Granger 1934- 英国经济
家 2003诺贝尔奖得主。发现非稳定(non-stationary)时间数列的特别组合可以呈现出稳定性，从而可以得出正确的统计
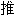理。他称此是一种“共合体”(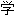术上译为协整cointegration)现象，并提出了根据同趋势(common trends)进行经济时间序列(time series)分析的方式。瑞典皇家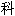
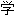
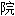说，格兰杰的发现对研究财富与消费、汇率与价格以及短期利率与长期利率之间的关系具有非常重要意义。克莱
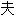。男子名。 Fr helper cop yright用户正在搜索
Geldstabilität, Geldstillegung, Geldstrafe, Geldstrafen, geldstrafen verhängen, Geldstück, Geldsumme, Geldsummen, Geldtasche, Geldtheorie,
相似单词
CLIST, Clitoral Hood, clitoridotomy, clitoris, Clive, Clive W.J. Granger, Clivia, CLK, CLLM, CLNP,
① 格兰杰。姓氏。
② 农夫。
Clive W.J. Granger 1934- 英国经济学家 2003诺贝尔奖
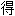主。发现非稳定(non-stationary)时间数列的特别组
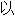呈现出稳定性，从而出正确的统计理。他称此是一
“
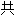
体”(学术上译为协整cointegration)现象，并提出了根据同趋势(common trends)进行经济时间序列(time series)分析的方式。瑞典皇家科学院说，格兰杰的发现对研究财富与消费、汇率与价格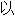及短期利率与长期利率之间的关系具有非常重要意义。克莱夫。男子名。 Fr helper cop yright
用户正在搜索
Geldunterschlagung, Geldverdienen, Geldverdiener, Geldverfassung, Geldverkehr, Geldverlegenheit, Geldverleiher, Geldverlust, Geldvermögen, Geldvermögenswert,
相似单词
CLIST, Clitoral Hood, clitoridotomy, clitoris, Clive, Clive W.J. Granger, Clivia, CLK, CLLM, CLNP,
① 格兰杰。姓氏。
②
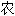
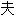。Clive W.J. Granger 1934- 英国经济
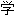
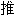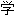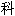
2003诺贝尔奖得主。发现非稳定(non-stationary)时间数列的特别组合可以呈现出稳定性，从而可以得出正确的统计理。他称此是一种“共合体”(术上译为协整cointegration)现象，并提出了根据同趋势(common trends)进行经济时间序列(time series)分析的方式。瑞典皇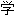院说，格兰杰的发现对研究财富与消费、汇率与价格以及短期利率与长期利率之间的关系具有非常重要意义。克莱
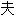。男子名。 Fr helper cop yright用户正在搜索
Geldwechsel, Geldwechseln, Geldwechselstelle, Geldwechsler, Geldwert, Geldwertminderung, Geldwertpapier, Geldwertstabilität, Geldwesen, Geldwirtschaft,
相似单词
CLIST, Clitoral Hood, clitoridotomy, clitoris, Clive, Clive W.J. Granger, Clivia, CLK, CLLM, CLNP,
① 格兰杰。姓氏。
② 农夫。
Clive W.J. Granger 1934- 英国经济学家 2003诺贝尔奖得主。发
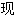非稳定(non-stationary)时间数列的特别组合
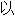
出稳定性，从而得出正确的统计理。他称此是一种“共合体”(学术上译为协
cointegration)
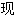
，并提出了根据同趋势(common trends)进行经济时间序列(time series)分析的方式。瑞典皇家科学院说，格兰杰的发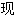对研究财富与消费、汇率与价格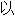及短期利率与长期利率之间的关系具有非常重要意义。克莱夫。男子名。 Fr helper cop yright
用户正在搜索
gelegen, Gelegenheit, Gelegenheiten, Gelegenheitsarbeit, Gelegenheitsarbeiter, Gelegenheitsdichter, Gelegenheitsdichtung, Gelegenheitsdieb, Gelegenheitsgedicht, Gelegenheitsgesellschaft,
相似单词
CLIST, Clitoral Hood, clitoridotomy, clitoris, Clive, Clive W.J. Granger, Clivia, CLK, CLLM, CLNP,
① 格兰杰。姓氏。
② 农夫。
Clive W.J. Granger 1934- 英国经济学家 2003
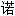
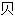
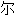奖得主。发现非稳定(non-stationary)时间数列
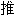特别组合可以呈现出稳定性，从而可以得出正确统计理。他称此是一种“共合体”(学术上译为协整cointegration)现象，并提出了根据同趋势(common trends)进行经济时间序列(time series)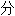
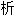
方式。瑞典皇家科学院说，格兰杰发现对研究财富与消费、汇率与价格以及短期利率与长期利率之间关系具有非常重要意义。克莱夫。男子名。 Fr helper cop yright
用户正在搜索
Gelehrsamkeit, gelehrt, Gelehrte, Gelehrte(r), Gelehrte[r], gelehrten, Gelehrtenfamilie, gelehrtenhaft, Gelehrtheit, Gelehtenwelt,
相似单词
CLIST, Clitoral Hood, clitoridotomy, clitoris, Clive, Clive W.J. Granger, Clivia, CLK, CLLM, CLNP,
用户正在搜索
Geleitschiff, Geleitschutz, Geleitsherr, Geleitsmann, Geleitwort, Geleitzug, Gelelektrophorese, gelenk, Gelenk, Gelenk-,
相似单词
CLIST, Clitoral Hood, clitoridotomy, clitoris, Clive, Clive W.J. Granger, Clivia, CLK, CLLM, CLNP,
用户正在搜索
Gelenkknarre, Gelenkknochen, Gelenkkompensator, Gelenkkoordinate, Gelenkkoordinaten, Gelenkkoordinatensystem, Gelenkkopf, Gelenkkörper, Gelenkkraft, Gelenkkraftfahrzeug,
相似单词
CLIST, Clitoral Hood, clitoridotomy, clitoris, Clive, Clive W.J. Granger, Clivia, CLK, CLLM, CLNP,
① 格兰杰。姓氏。
② 农夫。
Clive W.J. Granger 1934- 英国经济学家 2003诺贝尔奖得主。发现非稳定(non-stationary)时间数列的特
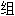
可以呈现
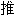稳定性，从而可以得正确的统计理。他称此是一种“共体”(学术上译为协整cointegration)现象，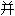
了根据同趋势(common trends)进行经济时间序列(time series)分析的方式。瑞典皇家科学院说，格兰杰的发现对研究财富与消费、汇率与价格以及短期利率与长期利率之间的关系具有非常重要意义。克莱夫。男子名。 Fr helper cop yright
用户正在搜索
Gelenkschlüssel, Gelenkschmerz, Gelenkschmiere, Gelenkschraube, Gelenkspalt, Gelenkspiel, Gelenkspindel, Gelenkspindelbohrmaschine, Gelenkspindelhalter, Gelenkstahlkappe,
相似单词
CLIST, Clitoral Hood, clitoridotomy, clitoris, Clive, Clive W.J. Granger, Clivia, CLK, CLLM, CLNP,
① 格兰杰。姓氏。
② 农夫。
Clive W.J. Granger 1934- 英国经济学家 2003诺贝尔奖得主。发
非稳定(non-stationary)时间数列的特别组合出稳定性，从而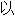得出正确的统计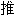理。他称此是一种“共合体”(学术上译为协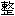cointegration)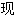，并提出了根据同趋势(common trends)进行经济时间序列(time series)分析的方式。瑞典皇家科学院说，格兰杰的发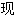对研究财富与消费、汇率与价格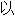及短期利率与长期利率之间的关系具有非常重要意义。克莱夫。男子名。 Fr helper cop yright
用户正在搜索
Gelenkteil, Gelenkteleskopbühne, gelenktemperatur, Gelenkträger, Gelenkturm, Gelenkverankerung, Gelenkverbindung, Gelenkverschluß, Gelenkverspannung, Gelenkversteifung,
相似单词
CLIST, Clitoral Hood, clitoridotomy, clitoris, Clive, Clive W.J. Granger, Clivia, CLK, CLLM, CLNP,
① 格兰杰。姓氏。
② 农夫。
Clive W.J. Granger 1934- 英国经济学家 2003诺贝尔奖
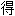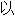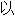
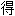
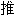主。发现非稳定(non-stationary)时间数列的特别组合可呈现稳定性，从而可正确的统计理。他称此是
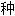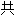“合体”(学术上译为协整cointegration)现象，并提了根据同趋势(common trends)进行经济时间序列(time series)分析的方式。瑞典皇家科学院说，格兰杰的发现对研究财富与消费、汇率与价格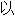及短期利率与长期利率之间的关系具有非常重要意义。克莱夫。男子名。 Fr helper cop yright
用户正在搜索
Gelenkwellenlager, gelenkwellenmittelstück, gelenkwellenmittelstücks, Gelenkwellenprüfstand, Gelenkwellenrohr, Gelenkwellenschutz, Gelenkwellenübertragung, Gelenkwellenverbindung, Gelenkwellenwinkel, Gelenk-Zahnstangen-getriebe, Gelenkzapfen, Gelenkzug, Gelenkzündkerzenschlüssel, gelernt, gelesen, Geleucht, Gelfett, Gelfiltration, gelförmig, Gelgenhumor, Gelichter, geliebt, Geliebte, Geliebte(r), Geliebter, geliedern, geliefert, geliehen, gelieren, Gelierharz,
相似单词
CLIST, Clitoral Hood, clitoridotomy, clitoris, Clive, Clive W.J. Granger, Clivia, CLK, CLLM, CLNP,
① 格兰杰。姓氏。
② 农夫。
Clive W.J. Granger 1934- 英国经济
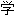家 2003诺贝尔奖得主。发现非稳
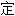(non-stationary)时间数列的特别组合可以呈现出稳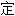
，
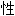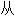而可以得出正确的统计
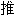理。他称此是一种“共合体”(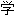
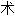
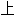译为协整cointegration)现象，并提出了根据同趋势(common trends)进行经济时间序列(time series)分析的方式。瑞典皇家科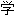院说，格兰杰的发现对研究财富与消费、汇率与价格以及短期利率与长期利率之间的关系具有非常重要意义。克莱夫。男子名。 Fr helper cop yright
用户正在搜索
gelinde, gelingen, gelingt es, gelitten, Gelkinetik, gell, gelle, gellen, gellend, Gellert,
相似单词
CLIST, Clitoral Hood, clitoridotomy, clitoris, Clive, Clive W.J. Granger, Clivia, CLK, CLLM, CLNP,